2D Vortex Dynamics
ff">
2D Vortex Dynamics
A pure electron plasma in a cylindrically symmetrical Penning trap is an ideal system
for the study of 2D vortex dynamics and 2D turbulence. Conservation of angular momentum means
that even when the plasma undergoes a violent instability, it is not lost from the system.
Thus, we are able to study turbulent processes from inception, through the nonlinear stages,
and finally to a stage of decaying noise fluctuations. The experiments are typically carried
out in the regime where the axial bounce frequency of an electron is large compared to the
ExB drift rotation frequency ( _b>>
_b>> _r), so the low frequency collective phenomena
(e.g., diocotron modes and turbulence) can be described by bounce-average
ExB drift dynamics. Since the column is long enough that z-dependence can be
neglected in Poisson's equation, the plasma evolution is to a good
approximation governed by the 2D drift-Poisson equations
_r), so the low frequency collective phenomena
(e.g., diocotron modes and turbulence) can be described by bounce-average
ExB drift dynamics. Since the column is long enough that z-dependence can be
neglected in Poisson's equation, the plasma evolution is to a good
approximation governed by the 2D drift-Poisson equations
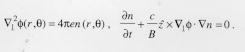
Interestingly, these equations are isomorphic to the equations which describe the 2D evolution of
an ideal (incompressible and inviscid) fluid: the electric potential corresponds to the stream
function and the electron density to the vorticity. The boundary condition on the electric
potential at the cylindrical wall corresponds to a free slip boundary condition in the fluid
problem. Thus, the electron plasma models the 2D dynamics of an ideal fluid. These equations
are also closely related to the Hasegawa-Mima equation for drift-wave modes in neutral plasmas.
In the vortex experiments, we create several isolated, finite-size vortices (i.e., electron
columns) ab initio. Here, the nonlinear dynamics of vortex interaction, filamentation,
and instability can be studied under ideal conditions. The evolution of the vorticity can be
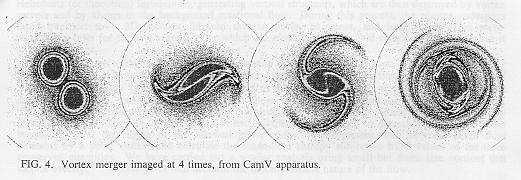
directly observed by measuring the electron density n(r, ,t). For example, the time
required for 2 symmetric vortices to merge is observed to vary from 1 orbit time to 10^4 orbit
times as their separation varies from 1.4 to 1.7 vortex diameters. This critical separation
distance is observed to scale with the radii of the vortices, as expected theoretically. In order
to properly characterize this data, we have had to establish a valid measure of the "radius" of
an extended vorticity profile; this measure is applicable to standard fluid vortices also.
An example of vortex merger imaged on the new CamV apparatus is shown in Fig.4.
,t). For example, the time
required for 2 symmetric vortices to merge is observed to vary from 1 orbit time to 10^4 orbit
times as their separation varies from 1.4 to 1.7 vortex diameters. This critical separation
distance is observed to scale with the radii of the vortices, as expected theoretically. In order
to properly characterize this data, we have had to establish a valid measure of the "radius" of
an extended vorticity profile; this measure is applicable to standard fluid vortices also.
An example of vortex merger imaged on the new CamV apparatus is shown in Fig.4.
We recently extended these vortex merger experiments to vortices with unequal radius and/or
vorticity. The two vortices are still observed to merge rapidly when they are closer than a
critical separation, and to stay separated for hundreds of orbits when the separation is slightly
larger. Merger is accompanied by the formation of filamentary arms, and results ultimately in an
axisymmetric central core surrounded by a lower density halo. Measurements of the critical
separation are in general agreement with extended vortex models, and the measurements of
the amount of vorticity ejected into the halo support a simple theoretical postulate. Here, the
experiments bear directly on theories of turbulent evolution due to consolidation of vortices
into fewer but larger vortices.
When vortices are too far apart to merge, it is common to treat them as point vortices.
In a recent series of experiments, we established that point vortex theory accurately describes
the equilibrium and stability properties of two extended vortices. This is the first time
that 2D fluid vortex motions have been measured with such precision, and it establishes that the
internal motions of the vortices can be effectively decoupled from the center-of-mass motions.
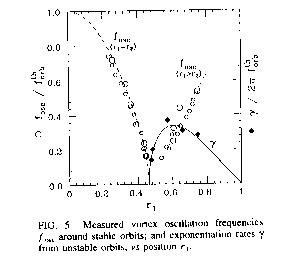
Both the oscillation frequencies Fosc around stable equilibria and the exponentiation rates
gamma away from unstable equilibria were measured, versus the radial position
r1 of a vortex, as shown in Fig. 5.
Experiments on modes and instabilities of isolated electron vortices have
established several limitations to standard 2D fluid theory.
First, it was found that the observed modes are poorly modeled by
the traditional "stair-step" vorticity profiles; full numerical analysis
of smooth profiles is needed. Second, an exponentially unstable m=1 diocotron mode
was observed, whereas traditional theory predicts no instability, and an initial-value
analysis predicts weak algebraic growth. Recently, we have analyzed the effects of finite
column length and finite Larmor radius effects, and found that exponential instability may arise
from either of these two effects.
Return to Theory Page
 _b>>
_b>> _r), so the low frequency collective phenomena
(e.g., diocotron modes and turbulence) can be described by bounce-average
ExB drift dynamics. Since the column is long enough that z-dependence can be
neglected in Poisson's equation, the plasma evolution is to a good
approximation governed by the 2D drift-Poisson equations
_r), so the low frequency collective phenomena
(e.g., diocotron modes and turbulence) can be described by bounce-average
ExB drift dynamics. Since the column is long enough that z-dependence can be
neglected in Poisson's equation, the plasma evolution is to a good
approximation governed by the 2D drift-Poisson equations

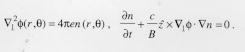
 ,t). For example, the time
required for 2 symmetric vortices to merge is observed to vary from 1 orbit time to 10^4 orbit
times as their separation varies from 1.4 to 1.7 vortex diameters. This critical separation
distance is observed to scale with the radii of the vortices, as expected theoretically. In order
to properly characterize this data, we have had to establish a valid measure of the "radius" of
an extended vorticity profile; this measure is applicable to standard fluid vortices also.
An example of vortex merger imaged on the new CamV apparatus is shown in Fig.4.
,t). For example, the time
required for 2 symmetric vortices to merge is observed to vary from 1 orbit time to 10^4 orbit
times as their separation varies from 1.4 to 1.7 vortex diameters. This critical separation
distance is observed to scale with the radii of the vortices, as expected theoretically. In order
to properly characterize this data, we have had to establish a valid measure of the "radius" of
an extended vorticity profile; this measure is applicable to standard fluid vortices also.
An example of vortex merger imaged on the new CamV apparatus is shown in Fig.4.
