Collisional Transport

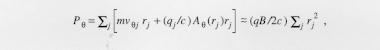
The most important concept for discussing radial particle transport in a non-neutral plasma is the total canonical angular momentum of the charged particles. This is

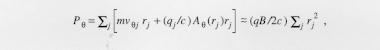
with A_(r)=Br/2 since the diamagnetic field is negligible compared to B. For the densities, electron velocities and magnetic fields considered here, only the (r_j)² term needs to be kept. Then, in the absence of external torques, the plasma cannot increase its mean square radius.

There are a number of physical effects which can apply a torque on the particles and cause radial expansion of the plasma, and we have previously quantified many of these processes. In the regime of high neutral pressure, the dominant torque is due to electron collisions with neutral atoms. For lower neutral pressure, the dominant torque is generally due to asymmetric electric or magnetic confinement field errors. The torque due to finite wall resistance and the angular momentum removed by cyclotron radiation is typically negligible.

Transport processes which conserve total angular momentum are also important and readily studied. Given enough time like-particle collisions bring the plasma to a true 3D thermal equilibrium state, through various types of effective "viscosity." see page on Viscous Transport.

We are presently analyzing and observing cross-field transport which arises due to compressional (or "second") viscosity acting on length changes in the plasma column. The length changes are driven by ExB drift rotation in the presence of asymmetric end potentials. Consider a long plasma column that is contained axially with end potentials that vary azimuthally. As a flux tube of plasma undergoes ExB drift rotation about the center of the column, the length of the tube oscillates about some mean value, and the p_par*dV work produces a corresponding oscillation in T_par. In turn, the collisional relaxation of T_par toward T_perp produces a slow dissipation of electrostatic energy into heat and a consequent radial expansion (cross field transport) of the plasma. We call the mechanism rotational pumping, by analogy with magnetic pumping.

We are making detailed comparisons between theory and experiment for the case where the end asymmetries are produced by displacing the column off axis, that is, by exciting an m=1 diocotron mode. In this case, the cross field transport implies a damping of the mode. Because the trap itself is cylindrically symmetric, the canonical angular momentum of the plasma is conserved. Thus, the displacement of the column off-axis must decrease as the plasma expands. 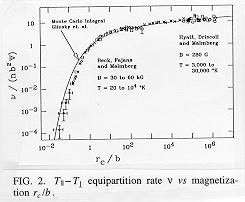We find a damping rate that is proportional to _perp,par the collisional equipartition rate. Interestingly, the magnetic field strength enters the damping rate only through the dependence of _perp,par on r_c /b(see Fig.2). Thus, as the field strength is increased (and r_c/b decreased), the damping rate is nearly independent of field strength until the regime of strong magnetization is reached (i.e., r_c/b<1) and then drops off dramatically.

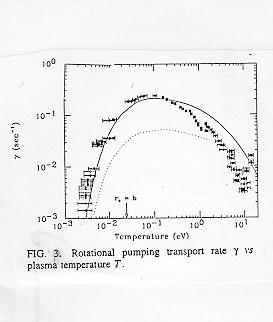
This signature was clearly observed in experiments carried out with the CV apparatus. The measured rate is nearly independent of B in the weakly magnetized regime. Figure 3 shows the measured (points) and predicted (curves) rates as a function of temperature; the rates drop dramatically in accord with theory as T becomes small. To obtain quantitative agreement, the exact plasma end shapes from the 3D Poisson solutions must be used (solid curve); approximating the end shapes gives less accurate predictions (dotted curve). This is a case where the wide parameter regime of the CV apparatus helps importantly in identifying the underlying physics. In the experiments, the change in canonical angular momentum and energy are also carefully monitored. As expected, the change in angular momentum due to plasma expansion is just balanced by the change due to mode damping, and the change in electrostatic energy due to plasma expansion is balanced by the change in thermal energy.

Now that we have experimental evidence that rotational pumping can be the dominant transport mechanism, we plan to calculate such transport for many different situations and to compare the predictions to experiment. For example, a tilt of the magnetic field (relative to the trap axis) and a curvature of the field both lead to asymmetric end potentials, or more precisely, to variation of flux tube length during ExB drift motion. Simple estimates suggest that the cross field flux for both these cases will be proportional to the plasma length squared, a commonly observed scaling. It is also natural to ask if rotational pumping sets the lifetime of highly asymmetric and toroidal plasmas discussed later. In the toroidal case, both T_par and T_perp vary as a result of the poloidal ExB drift rotation.

A rotating asymmetry can be produced by careful phasing of the potentials applied to azimuthal sections of the wall or end rings. If the rotation is faster than the plasma, the rotating asymmetry produces a forward drag and an inward radial flux. We have preliminary experimental evidence that the forward drag can be larger than the backward drag due to ambient static asymmetries, so that the plasma can be confined indefinitely or the density can be increased. This process heats the plasma, so steady state can be achieved only if the plasma is also cooled, say through cyclotron radiation or through collisions with neutrals. We plan to study the effect of rotating asymmetries both theoretically and experimentally for both electron and ion plasmas.

For asymmetric plasmas, we also intend to analyze and measure the transport due to shear viscosity. The shear viscosity is thought to have contributions from long-range "ExB drift collisions", in addition to contributions from close velocity-scattering collisions; whereas only velocity-scattering contributes to the compressional viscosity. In the highly magnetized regime, velocity scatterings between parallel and perpendicular are suppressed, and the second viscosity goes to zero. We believe one can then directly measure the transport from the shear viscosity.

Other related experiments that take advantage of the wide operating parameter range of CV will also be pursued. For a number of years, we have observed (but not understood) "squeeze damping" of the m=1 diocotron mode. Here, an axisymmetric squeeze potential applied to the containment walls induces transport and axisymmetrization of the initially off-axis plasma, giving damping of the m=1 diocotron motion. The applied squeeze potential alters the axial bounce motion of individual electrons, so this effect is closely related to rotational pumping. However, we observe that squeeze damping occurs even in cryogenic plasmas, so a different irreversible process must be contributing.

Along a similar line, we observe weak damping of electron plasma waves even when the plasma is so cold that direct Landau damping should be negligible. Here, the damping rates are 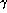/_p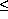10¯³, a range which is not easily investigated in other plasma systems. Various theories have suggested that there should be coupling between the compressional electron plasma waves and the ExB drift diocotron modes due to axial boundaries, but this effect has never been measured. Since we have a rather complete description of the 3D plasma equilibrium, we should be able to make definitive comparisons between theory and experiment in this system.

Similarly, the IV apparatus may clarify the processes involved in collisional relaxation to 3D thermal equilibrium. Here, the net particle transport is fourth order in spatial derivatives, due to the exact cancellation of particles undergoing second order diffusion in opposite directions. Measurement of test particle diffusion would be definitive in this regard. There is a large body of theoretical literature following the work of Taylor and McNamara and Okuda and Dawson that supports the theory that test particle transport will scale like B¯¹ rather than B¯². The traditional transport theories of test particle transport, where a particle steps one cyclotron radius per collision, gives a diffusion coefficient D=nu_ii*r_ci¯² B¯². In the T-M/O-D theories, the transport is due to ExB drifts associated with thermal levels of low frequency eddies, or vortices, and the diffusion coefficient is: