

We have recently determined analytically the cold fluid normal modes of a small cryogenic single species plasma in a Penning trap. This is the only analytic solution for the modes of a realistic finite confined magnetized plasma. In addition, the quadrupole modes have been analyzed in a fully nonlinear manner. When the plasma is distant from the walls, the thermal equilibrium state is a uniform density spheroid, i.e. an ellipsoid of revolution. A large amplitude quadrupole mode deforms the spheroidal plasma into a triaxial ellipsoid with time dependent shape and orientation. An analysis of the modes which are stationary equilibria in some rotating frame shows that the equilibria fall into two classes with quite different properties: the ellipsoids are either aligned or tilted with respect to the magnetic field. Some of these ellipsoidal equilibria have densities considerable larger than the well-known Brillouin limit for the density of a cylindrically- symmetric non-neutral plasma.
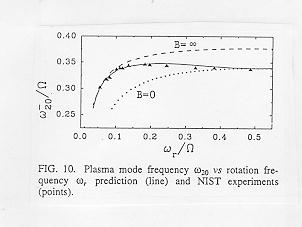
The frequency of the modes depends on the rotation frequency, plasma frequency and and plasma shape, so measurement of mode frequencies is a useful nondestructive plasma diagnostic, particularly for pure electron, pure positron or antiproton plasmasa where other nondestructive diagnostics are unavailable. This diagnostic has now been applied in several experiments in different groups (ie. Fig 10). However, in the cold fluid theory the effect of finite plasma pressure is neglected, and in at least one experiment thermal effects have been observed to shift the normal mode frequencies.
We propose to extend our normal mode analysis to account for these thermal effects. We already made some progress in this regard--a theory based on the ansatz that the warm plasma remains a uniform density spheroid, with slightly shifted shape and density due to pressure effects has recently been published, and works reasonable well to explain the thermal corrections of one particular normal mode. However, we wish to generalize this theory for other modes. We propose to employ a perturbation theory for the modes, keeping thermal corrections to the cold fluid equations as a perturbation, in order to determine to lowest order in plasma temperature the thermal effects on the modes.
Frequency shifts and mode damping have recently been observed in simulations of small bounded strongly correlated plasmas. We propose to exten our cold fluid theory for the normal modes to take correlations into account. Our approach will be similar to the perturbation approach described above--we will add correlation effects by includinga correlation pressure tensor in the fluid equations. This correlation pressure has three effect: 1)it causes a shift in the shape and density of the plasma equilibrium, which in turn shifts mode frequencies; 2)the extra restoring force due to the pressure also shifts the mode frequencies, i.e. a crystallized plasma has finite buld and shear moduli; 3)viscous terms in the pressure tensor cause damping of the modes. While there has been considerable work on such models for the case of infinite homgeneous plasma, we are unaware of any work which also includes boundary effects (the spheroidal plasma shape) which are essential here.
Although these effects have as yet been observed only in simulations of the modes, it should be possible to observe the correlation effects directly in experiments on laser cooled strongly correlated ion clouds, which would allow the first experimental determination of quantities such as bulk and shear moduli and viscosities in a strongly correlated magnetized plasma. Detailed theory predictions for these effects are of course essential for comparison to the experiments. Although derived with the strong correlation limit in mind, our predictions of frequency shifts due to thermal effects also apply to experiments on weakly correlated plasmas.